Kapitel 3: Das Aktivitätsdiagramm

Allround-Diagramme zur Darstellung von Abläufen

Das Aktivitätsdiagramm beschreibt ganz allgemein Abläufe. Es stellt dar, in welcher Reihenfolge ganz bestimmte Aktionen ausgeführt werden.

Alle Aktionen in einem Aktivitätsdiagramm beschreiben gemeinsam eine Aktivität. Das kann zum Beispiel ein Use-Case sein, aber auch eine in einer Programmiersprache entwickelte Funktion. Der Einsatz von Aktivitätsdiagrammen ist nicht auf die Darstellung von Zusammenhängen von Anforderungen beschränkt, sondern kann während des gesamten Softwareentwicklungsprozesses hilfreich sein. Aktivitätsdiagramme sind die Allround-Diagramme der UML, die immer dann eingesetzt werden können, wenn Abläufe übersichtlich dargestellt werden müssen.

In diesem Kapitel greifen wir auf Use-Cases zu, die im zweiten Kapitel Verwendung fanden, und stellen ihre internen Abläufe etwas genauer dar.

Von Knoten und Kanten und Token

Ein Aktivitätsdiagramm kennt grundsätzlich zwei Arten von Bausteinen: Knoten und Kanten. Knoten sind die Stellen, an denen etwas passiert. Kanten sind einfach nur die Verbindungslinien zwischen Knoten. Über diese Verbindungslinien wandern sogenannte Token. Was aber sind jetzt schon wieder Token?

Jedes Aktivitätsdiagramm hat einen oder mehrere Start- und Endpunkte. Diese beiden Punkte sind über viele Knoten und Kanten verbunden. Wenn nun eine Aktivität ausgeführt wird, stellt man sich vor, dass ein kleines Männchen im Startpunkt zu wandern beginnt. Dieses Männchen wandert die erste Verbindungslinie entlang zum ersten Knoten. Nachdem dort irgendetwas passiert ist, wandert das Männchen auf der von diesem Knoten ausgehenden Verbindungslinie zum zweiten Knoten. Diese Wanderung setzt es fort, bis es am Endpunkt des Diagramms ankommt, womit die Aktivität endet.

Während ich nun von einem Männchen gesprochen habe, wird in der UML der Begriff Token verwendet. Es handelt sich also um irgendetwas, das vom Startpunkt ausgehend durch das gesamte Aktivitätsdiagramm bis zum Endpunkt wandert. Stellen Sie sich den Token am besten als einen Punkt vor, der im Aktivitätsdiagramm immer anzeigt, wo momentan die Ausführung steht. Das Aktivitätsdiagramm stellt den Ablauf von Aktionen dar, und irgendwie muss ja angezeigt werden, welche Aktionen bisher ausgeführt wurden und als nächstes ausgeführt werden. Der Token zeigt Ihnen an, wo das Aktivitätsdiagramm momentan steht.

Während Kanten einfach nur durchgezogene Linien mit einer Pfeilspitze sind, die anzeigt, in welche Richtung auf dieser Linie Token wandern dürfen, gibt es unterschiedliche Arten von Knoten. Im Folgenden werden Ihnen die wichtigsten Knoten im Aktivitätsdiagramm vorgestellt.

Der Start- und Endknoten wurde bereits erwähnt: Hier startet und endet die Ausführung einer Aktivität. Bei Ausführung einer Aktivität beginnt im Startknoten genau ein Token zu wandern. Im Endknoten angekommen, der mit dem äußeren schwarzen Ring ein wenig an eine Zielscheibe erinnert, wird der Token zerstört.

Beachten Sie, dass es beliebig viele Start- und Endknoten in einem Aktivitätsdiagramm geben kann. Während mehrere Endknoten grundsätzlich kein Problem darstellen, verkomplizieren mehrere Startknoten ein Aktivitätsdiagramm: In diesem Fall bewegen sich nämlich mehrere Token gleichzeitig durch das Aktivitätsdiagramm, da in jedem Startknoten ein Token zu wandern beginnt. Mehrere Startknoten ermöglichen es, in einem Aktivitätsdiagramm den gleichzeitigen Ablauf von Aktionen darzustellen, was hin und wieder nützlich sein kann.

Beachten Sie außerdem, dass die Ausführung einer Aktivität dann endet, wenn der erste Token den Endknoten erreicht. Sollten sich zu diesem Zeitpunkt andere Token durch das Aktivitätsdiagramm bewegen, werden diese augenblicklich zerstört.

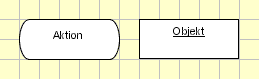
Der wichtigste Baustein im Aktivitätsdiagramm ist die Aktion, als Rechteck mit abgerundeten Ecken dargestellt. Aktionen stellen die einzelnen Schritte dar, aus denen eine Aktivität besteht. Man könnte sagen, sie sind die kleinste, nicht mehr zerlegbare Einheit einer Aktivität. Alle Aktionen zusammengenommen stellen einen schrittweisen Ablauf dar wie etwa den eines Use-Case oder einer Funktion.

Im Rechteck mit den abgerundeten Ecken wird jeweils eine kurze Beschreibung der Aktion angegeben. Diese Beschreibung sollte wie bei Use-Cases kurz und knapp und präzise sein.

Ein Rechteck ohne abgerundete Ecken stellt einen Objektknoten dar. Objektknoten symbolisieren Datenspeicher: Wenn sich ein Objektknoten zwischen zwei Aktionen befindet, transportiert das Token von der ausgehenden Aktion Daten in den Speicher und von dort in die nächste Aktion. Wenn Token also mit Objektknoten in Berührung kommen, transportieren sie die Daten, die im Objektknoten angegeben sind. In diesem Fall geben Token also nicht mehr nur an, wo sich die Ausführung einer Aktivität im Moment befindet. Sie richten darüberhinaus das Augenmerk auf Daten, die von einer Aktion an die nächste übergeben werden müssen.

Für ein besseres Verständnis stellen Sie sich Aktionen einfach als Funktionen vor: Die vorausgehende Aktion gibt ein Ergebnis aus, das als Eingabe an die nächste Aktion übergeben wird. Das Aktivitätsdiagramm wird an dieser Stelle also sehr viel präziser, weil es nicht mehr nur aussagt, dass eine Aktion der anderen folgt, sondern darüberhinaus ganz bestimmte Daten von einer Aktion an die nächste weitergegeben werden.

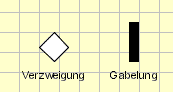
Wenn Sie Verbindungslinien verzweigen wollen, verwenden Sie einen der beiden oben abgebildeten Knoten: Die Raute stellt eine Verzweigung dar, der schwarze Balken eine Gabelung. Sie können diese beiden Knoten nicht nur verwenden, um eine Verbindungslinie aufzuteilen, sondern auch um mehrere Verbindungslinien zu einer zusammenzuführen.

Der Unterschied zwischen der Verzweigung und der Gabelung ist: Bei einer Verzweigung wird der Token auf genau einer der ausgehenden Verbindungslinien weitergeleitet. Bei einer Gabelung wird der Token kopiert, und auf jeder ausgehenden Verbindungslinie wandert eine Kopie des Tokens weiter.

Werden durch eine Verzweigung mehrere Verbindungslinien vereint, wandert jedes eingehende Token sofort auf der ausgehenden Verbindungslinie weiter. Werden durch eine Gabelung mehrere Verbindungslinien vereint, muss ein Token, das auf einer Verbindungslinie eingeht, darauf warten, bis auf allen eingehenden Verbindungslinien ein Token ankommt - erst dann wird auf der ausgehenden Verbindungslinie ein Token weitergeschickt.

An ausgehende Verbindungslinien können Bedingungen in eckigen Klammern gestellt werden. Auf diese Weise lässt sich angeben, wann ein Token zur Weiterfahrt eine Verbindungslinie nutzen darf.

Sehen Sie sich nun im Folgenden Aktivitätsdiagramme an, die Use-Cases aus dem Kapitel 2, Das Use-Case-Diagramm beschreiben und aus oben vorgestellten Bausteinen bestehen.

Den Pfeilen nach bis zum Ziel

Im Kapitel 2, Das Use-Case-Diagramm hatten wir als eine wesentliche Anforderung unseres Online-Shops herausgearbeitet, dass ein Kunde während des Bestellvorgangs seine Anschrift eingeben muss. Der Use-Case Anschrift eingeben soll nun durch ein Aktivitätsdiagramm etwas näher beleuchtet werden.

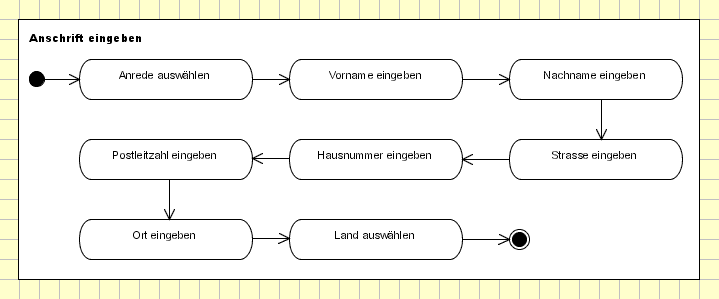
Ein Aktivitätsdiagramm wird häufig in ein Rechteck mit abgerundeten Ecken eingezeichnet. Da die für dieses Buch verwendete Modellierungssoftware keine abgerundeten Ecken darstellen kann, besitzen die Rechtecke der Aktivitätsdiagramme in diesem Buch keine abgerundeten Ecken. Das ist kein Beinbruch, da der UML-Standard die Darstellung des Rechtecks nicht festlegt. Er schreibt lediglich vor, dass links oben im Rechteck der Name der Aktivität stehen muss - in unserem Beispiel also Anschrift eingeben.

Unser Aktivitätsdiagramm Anschrift eingeben beschreibt den internen Ablauf des im zweiten Kapitel verwendeten Use-Case Anschrift eingeben. Das Aktivitätsdiagramm besteht aus acht Aktionen, die alle durch Pfeile verbunden sind. Der Startpunkt befindet sich links oben, der Endpunkt rechts unten im Aktivitätsdiagramm.

Stellen Sie sich nun vor, dass ein Kunde in unserem Online-Shop aufgefordert wird, seine Anschrift einzugeben - die Aktivität wird also gestartet. Zuerst wird ein Token im Startpunkt erzeugt, der die Verbindungslinie zum ersten Knoten entlang wandert. Der erste Knoten im Aktivitätsdiagramm ist mit Anrede auswählen beschriftet. Die erste Aktion des Kunden bei Eingabe seiner Anschrift ist es also, die Anrede aus einer Liste auszuwählen. Danach wandert der Token weiter zum Knoten Vorname eingeben. Ist diese Aktion ausgeführt, geht die Reise des Tokens zum Knoten Nachname eingeben. Der Token bewegt sich also Schritt für Schritt von einem Knoten zum nächsten, bis alle Aktionen durchlaufen sind und er am Endpunkt ankommt. Dort wird der Token zerstört. Da nur ein Token die ganze Zeit im Diagramm unterwegs war und dieser nun zerstört ist, ist die Aktivität beendet.

Das Aktivitätsdiagramm Anschrift eingeben sollte recht einfach zu verstehen sein. Wir sehen uns nun im Folgenden das Aktivitätsdiagramm zum Use-Case Anschrift überprüfen an. Das ist insofern interessanter als dass wir dort Verzweigungen einbauen müssen, da die Überprüfung der Anschrift je nach eingegebenen Daten positiv oder negativ ausfällt.

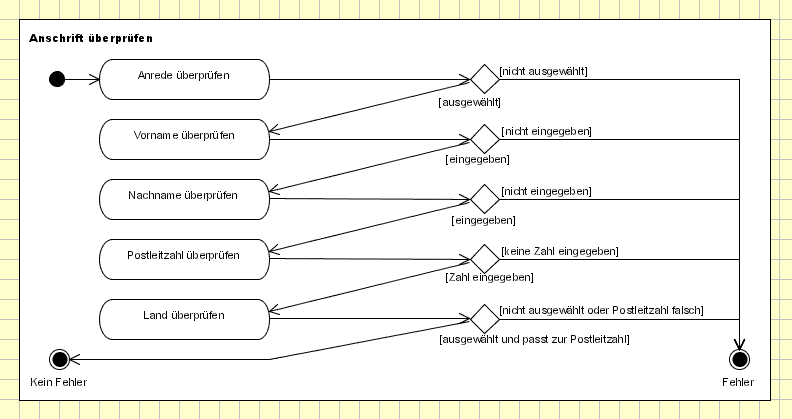
Bei diesem Aktivitätsdiagramm fällt auf, dass es zwei Endknoten besitzt: Einer ist mit Kein Fehler, der andere mit Fehler beschriftet. Das sollte insofern einleuchtend sein als dass die Überprüfung der Anschrift sowohl positiv als auch negativ ausfallen kann - je nachdem, ob der Anwender seine Daten vollständig und richtig eingegeben hat oder eben nicht.

Obiges Aktivitätsdiagramm überprüft nicht jede einzelne Eingabe, da sonst das Diagramm unnötig aufgebläht worden wäre. Es werden lediglich die Anrede, der Vor- und Nachname, die Postleitzahl und das Land überprüft.

Beginnen wir das Aktivitätsdiagramm links oben beim Startpunkt. Dort wird ein Token erstellt, der zur Aktion Anrede überprüfen wandert. Hier wird geprüft, ob der Anwender tatsächlich eine Anrede ausgewählt hat. Wir können natürlich nicht überprüfen, ob die Anrede richtig ist - der Anwender soll aber immerhin eine Anrede ausgewählt haben.

Wenn wir auf der von der Aktion Anrede überprüfen ausgehenden Verbindungslinie weiter wandern, gelangen wir zu einer Verzweigung. Von dieser Verzweigung gehen zwei Verbindungslinien weg. Jede Verbindungslinie ist mit einer Bedingung versehen, die in eckigen Klammern angegeben ist. Von dieser Bedingung hängt nun ab, auf welcher der beiden weiterführenden Verbindungslinien unser Token weiter wandern darf. Das Token muss die Verbindungslinie nach links unten zur Aktion Vorname überprüfen nehmen, wenn die Bedingung ausgewählt wahr ist. Anders gesagt: Wenn eine Anrede ausgewählt ist, muss der Token nach links unten weiter wandern. Ist jedoch keine Anrede ausgewählt, ist die Bedingung wahr, die an der nach rechts weiterführenden Verbindungslinie steht. In diesem Fall wandert der Token zu einem Endpunkt des Diagramms, der mit Fehler beschriftet ist. Die Überprüfung der anderen Angaben würde also abgebrochen, die Aktivität beendet.

Sollte der Anwender eine Anrede ausgewählt haben, wandert der Token zur Aktion Vorname überprüfen. Auch hier können wir lediglich überprüfen, ob der Anwender überhaupt etwas eingegeben hat - ob die Eingabe tatsächlich sein Vorname ist, wissen wir natürlich nicht.

Wenn wir von dieser Aktion weiter wandern, gelangen wir wieder zu einer Verzweigung. Der Token muss sich wieder für die weiterführende Verbindungslinie entscheiden, dessen Bedingung wahr ist. Ist ein Vorname eingegeben worden, muss das Token nach links unten zur Aktion Nachname überprüfen wandern, andernfalls zum Endpunkt Fehler.

Beachten Sie, dass zu überprüfende Bedingungen so festgelegt werden müssen, dass immer eindeutig ist, welche ausgehende Verbindungslinie gewählt werden muss. Es darf nicht sein, dass mehrere Bedingungen gleichzeitig zutreffen und ein Token nicht weiß, auf welcher Verbindungslinie es eigentlich nun seinen Weg fortsetzen muss.

In diesem Aktivitätsdiagramm ist hinter jeder Aktion eine Verzweigung angegeben, von der abhängt, ob die Überprüfung der Anschrift fortgesetzt wird oder mit einem Fehler abgebrochen wird. Sind die Überprüfungen jeweils erfolgreich, gelangt der Token schlußendlich zum Endknoten Kein Fehler, womit die Aktivität endet.

Im folgenden Aktivitätsdiagramm sehen Sie, wie die Gabelung verwendet wird.

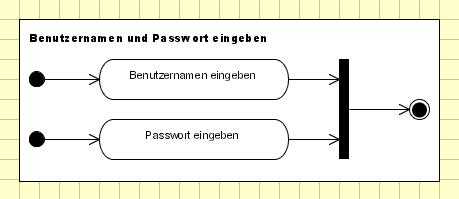
Obiges Aktivitätsdiagramm beschreibt den im zweiten Kapitel erwähnten Use-Case Benutzernamen und Passwort eingeben. In diesem Aktivitätsdiagramm tauchen zwei Startknoten auf, was bedeutet: Wenn diese Aktivität ausgeführt wird, wandern zwei Token durch das Diagramm, da von jedem Startknoten ein Token ausgeworfen wird.

Die beiden Token wandern zu den Aktionen Benutzernamen eingeben und Passwort eingeben. Wenn eine dieser beiden Aktionen beendet ist und der Anwender entweder zuerst seinen Benutzernamen oder aber das Passwort eingegeben hat, wandert der Token von dieser Aktion zur Gabelung. Von der Gabelung wissen wir, dass ein Token erst dann auf der ausgehenden Verbindungslinie weiter wandern darf, wenn an allen eingehenden Verbindungslinien Token ankommen. Da der Anwender wie angenommen bisher erst eine Aktion ausgeführt hat, wartet also nun ein Token an der Gabelung auf das andere Token. Erst wenn der Anwender auch die andere Aktion ausgeführt hat, wandert von dort der Token zur Gabelung, von der dann ein Token zum Endknoten des Aktivitätsdiagramms laufen darf.

Dieses Aktivitätsdiagramm sagt folgendes aus: Es spielt keine Rolle, in welcher Reihenfolge die Eingaben vom Anwender vorgenommen werden. Es müssen jedoch beide Eingaben vorgenommen werden, damit die Aktivität beendet wird.

Da wir es mit einem Online-Shop zu tun haben, ist das Aktivitätsdiagramm durchaus einleuchtend. Wenn wir uns eine Webseite vorstellen, auf der der Distributor seinen Benutzernamen und sein Passwort eingeben soll, wird diese Webseite zwei Eingabeschaltflächen zur Verfügung stellen. Es kann uns und dem Online-Shop egal sein, ob der Distributor zuerst seinen Benutzernamen oder zuerst sein Passwort eingibt. Wichtig ist nur, dass beim Absenden des Login-Formulars tatsächlich beide Angaben vorhanden sind. Die Reihenfolge der Eingaben spielt jedoch keine Rolle.

Genaugenommen läuft die Eingabe einer Anschrift ähnlich ab: Auch hier interessiert uns nicht, in welcher Reihenfolge Kunden ihre Daten eingeben. Das in diesem Kapitel vorgestellte Aktivitätsdiagramm zum Use-Case Anschrift eingeben wird daher nun wie folgt geändert.

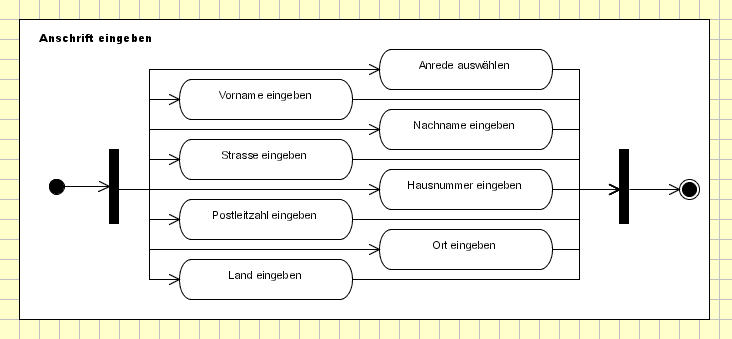
Wir haben nun zwei Gabelungen in das Aktivitätsdiagramm eingebaut. An der ersten Gabelung, die sich direkt hinter dem Startknoten auf der linken Seite des Diagramms befindet, wird der Token multipliziert. Auf jeder von der Gabelung ausgehenden Verbindungslinie wandert nun ein Token weiter zur entsprechenden Aktion. Hinter den Aktionen werden alle Verbindungslinien wieder zusammengeführt und durch eine weitere Gabelung gebündelt. An dieser Gabelung wird erst dann ein Token zum Endknoten weitergeschickt, wenn an allen eingehenden Verbindungslinien Token vorliegen. Das heißt also: Die Aktivität wird erst dann beendet, wenn alle Aktionen durchlaufen wurden - in welcher Reihenfolge spielt keine Rolle.

Beachten Sie, dass es prinzipiell keinen Unterschied macht, ob Sie einen Startkoten mit dahinterliegender Gabelung verwenden oder aber mehrere Startknoten - beides führt dazu, dass mehrere Token gleichzeitig durch das Diagramm wandern.

Da dies für Ihr Verständnis für den gleichzeitigen Ablauf von Aktionen wichtig sein kann: Token bewegen sich unendlich schnell über Verbindungslinien. Lange Verbindungslinien bedeuten also nicht, dass ein Token länger unterwegs ist als auf kurzen Verbindungslinien. Verbindungslinien sind nur ein Hilfsmittel, um zu verstehen, in welcher Reihenfolge und nach welchen Regeln Aktionen hintereinander ausgeführt werden. Token flitzen über diese Verbindungslinien aber unendlich schnell: Wenn eine Aktion beendet ist und der Token aus dem entsprechenden Knoten austritt, kommt er quasi im gleichen Moment am nächsten Knoten an, wo die nächste Aktion augenblicklich gestartet wird.

Lediglich innerhalb von Knoten können sich Token beliebig lange aufhalten. Denken Sie zum Beispiel an obiges Aktivitätsdiagramm, in dem Aktionen erst dann beendet sind, wenn der Anwender auch tatsächlich die entsprechende Eingabe vorgenommen hat. Solange Aktionen nicht ausgeführt sind, wartet der Token im Knoten.

Wenn Sie sich wundern, warum hinter der Gabelung Verbindungslinien ohne Verzweigung gesplittet und vor der Gabelung Verbindungslinien ebenfalls ohne Verzweigung zusammengeführt werden, so haben Sie gut aufgepasst: Das Diagramm ist etwas schlampig gezeichnet. Eigentlich müssten alle Verbindungslinien getrennt verlaufen und einzeln an der ersten Gabelung beginnen bzw. an der zweiten Gabelung enden. Da dies aber jeweils acht Linien wären, sind sie jeweils kurz hinter und vor der Gabelung gebündelt worden. Über diese Darstellung kann man zu Recht meckern, wenn man sich strikt an die UML halten möchte.

Vergessen Sie aber nicht, dass der wichtigste Grund, warum wir Software modellieren und UML-Diagramme anwenden, der ist, dass wir uns von dieser Vorgehensweise und diesen Instrumenten einen Nutzen versprechen. Wenn die Darstellung wie im obigen Diagramm für den Softwaremodellierer nützlicher, weil zum Beispiel übersichtlicher ist, dann soll er sich für diese Darstellungsform entscheiden - vorausgesetzt es sprechen keine anderen wichtigen Gründe dagegen wie zum Beispiel eine koordinierte Softwareentwicklung im Team, wo nicht jeder Softwareentwickler nach Gutdünken UML-Diagramme abwandeln kann.

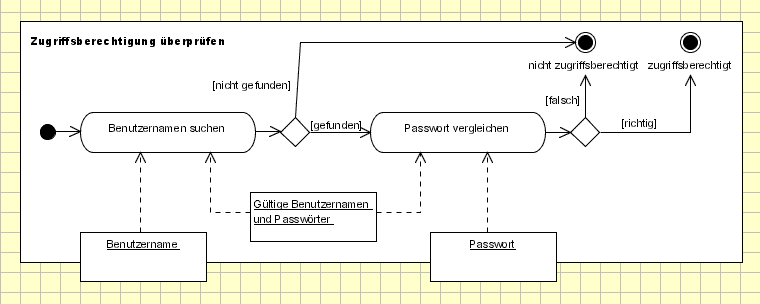
Obiges Aktivitätsdiagramm beschreibt den Ablauf des Use-Cases Zugriffsberechtigung überprüfen. Hier wird erstmals mit Objektknoten gearbeitet. Beachten Sie, dass dieses Aktivitätsdiagramm für die Darstellung von Anforderungen eher untypisch ist. Denn bei Anforderungen geht es vorrangig um das, was das System tut, nicht um das Wie. Die Frage, wie Daten verarbeitet werden - Objektknoten stellen ja Daten dar - spielt eher bei der Implementierung des Systems eine Rolle. Im obigen Aktivitätsdiagramm werden Objektknoten lediglich verwendet, damit Sie sehen, wie deren Einsatz in der Praxis aussieht.

Objektknoten erkennen Sie an Rechtecken ohne abgerundete Ecken. Im obigen Aktivitätsdiagramm werden demnach drei Objektknoten verwendet. Merkwürdigerweise stehen die zwei Objektknoten Benutzername und Passwort nicht vollständig im Aktivitätsdiagramm, sondern gucken über den Rand hinaus.

Erinnern Sie sich, dass wir sagten, Aktivitätsdiagramme können den Ablauf von Use-Cases oder auch Funktionen beschreiben? Wenn Sie sich obiges Aktivitätsdiagramm als eine Funktion vorstellen, bedeuten die beiden Objektknoten, die auf dem Rand liegen, dass diese Funktion zwei Parameter erwartet - nämlich die Eingabe eines Benutzernamens und eines Passworts. Dass es sich um Eingabeparameter handelt, erkennen Sie daran, dass die Verbindungslinien von diesen beiden Objektknoten wegführen. Würden die Verbindungslinien auf die beiden Objektknoten zeigen, würde das bedeuten, dass die Aktivität Ergebnisse ausgibt - auch das ist möglich.

Wenn die Aktivität ausgeführt wird, läuft ein Token vom Startknoten zur ersten Aktion Benutzername suchen. Diese Aktion erhält darüberhinaus zwei Token mit Daten: Ein Token hat seinen Ursprung im Objektknoten Benutzername, der andere Token im Objektknoten Gültige Benutzernamen und Passwörter.

Objektknoten, die auf dem Rand des Aktivitätsdiagramms liegen, sind Ein- oder Ausgabeparameter. Handelt es sich so wie hier um Eingabeparameter, geht man davon aus, dass beim Start der Aktivität entsprechende Daten in diesen Objektknoten vorliegen und diese per Token in das Aktivitätsdiagramm hinein transportiert werden. Diese Token entstehen also in den Objektknoten selbst und transportieren von dort Daten zum nächsten Knoten. Auf diese Weise wird also im obigen Diagramm zur ersten auszuführenden Aktion Benutzername suchen der Benutzername transportiert, der von außen an die Aktivität übergeben wird. Das ist der Benutzername, den der Distributor im Use-Case Benutzername und Passwort eingeben eingegeben hat.

Der vom Objektknoten gelieferte Benutzername muss nun gegenüber irgendetwas überprüft werden, um festzustellen, ob dieser Benutzername tatsächlich gültig ist. Dazu transportiert ein anderer Token vom Objektknoten Gültige Benutzernamen und Passwörter sämtliche im System bekannte Benutzernamen-Passwort-Kombinationen zur Aktion Benutzernamen suchen. Diese kann dann den vom einen Objektknoten erhaltenen Benutzernamen in der Liste aller Benutzernamen-Passwort-Kombinationen suchen. Abhängig vom Ergebnis wird zur nächsten Aktion Passwort vergleichen verzweigt oder aber zum Endknoten nicht zugriffsberechtigt. Die Aktion Passwort vergleichen arbeitet analog zur Aktion Benutzernamen suchen.

Beachten Sie, dass vom Objektknoten Gültige Benutzernamen und Passwörter zwei Verbindungslinien ausgehen. Dies entspricht einer Verbindungslinie, die mit einer Gabelung verbunden ist. Auf beiden Verbindungslinien transportiert also jeweils ein Token Daten vom Objektknoten zur anliegenden Aktion. So kann die Aktion Benutzernamen suchen nachgucken, ob der vom Distributor eingegebene Benutzername bekannt ist, und die Aktion Passwort vergleichen kann das eingegebene Passwort mit dem vergleichen, das zum gefundenen Benutzernamen gehört.

Das Allround-Diagramm der Verhaltensdiagramme

So schön und einleuchtend Aktivitätsdiagramme auch sein mögen, so sind es doch nur Hilfsmittel, um sich einen Überblick über komplexe Abläufe vor der Programmierung zu verschaffen. Um die Programmierung dieser Abläufe kommen Sie nicht herum. Viele Entwickler haben daher Schwierigkeiten, sich mit der UML anzufreunden: Es scheint als macht man alles doppelt. Zuerst zeichnet man Abläufe in Aktivitätsdiagrammen auf, danach muss man sie in einer Programmiersprache nochmal erstellen.

Das Aktivitätsdiagramm der UML ist ein Hilfsmittel, um Abläufe schrittweise und übersichtlich darzustellen. Das bedeutet jedoch nicht, dass Sie nun alles, was Sie finden können, in Aktivitätsdiagrammen darstellen sollen. Wenn Ihnen bestimmte Abläufe auch ohne Aktivitätsdiagramm klar sind, brauchen Sie natürlich kein Aktivitätsdiagramm erstellen. Wenn Sie jedoch vor der Eingabe der ersten Zeile des Quellcodes alle komplizierten Abläufe durch Aktivitätsdiagramme dargestellt und durchdacht haben, brauchen Sie bei der Programmierung nur noch Ihre Aktivitätsdiagramme in die Programmiersprache übersetzen. Alle Probleme und Schwierigkeiten wurden ja bereits vorher gelöst.

Tatsächlich bieten Aktivitätsdiagramme viel mehr Bausteine an als in diesem Buch vorgestellt werden können - Bausteine, die sehr stark an Kontrollstrukturen erinnern, wie sie in vielen Programmiersprachen Verwendung finden. Ziel ist es, eines Tages quasi per Knopfdruck Abläufe, die in einem Aktivitätsdiagramm abgebildet sind, in Quellcode zu übersetzen. Von diesem Ziel ist man noch weit entfernt. Eine direkte Übersetzung von Diagrammen in Quellcode ist heutzutage eigentlich nur bei Klassendiagrammen möglich. Klassendiagramme lernen Sie im Kapitel 4, Das Klassendiagramm kennen, die Code-Generierung - also das Erstellen von Quellcode per Knopfdruck auf Basis von Klassendiagrammen - im Kapitel 5, Code-Generierung.